BIOL245 General Ecology Exam #2 KEY
Fall 1998
Your answers to these questions should be complete, yet succinct. Extraneous
material will count against you. Show all work for the problems,
and label the axes of your graphs. Each correct answer is worth
five points unless otherwise noted.
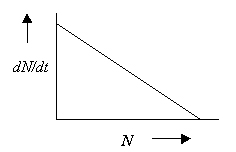
1. Define and illustrate graphically population regulation.
Regulation is homeostasis, which in populations is the negative feedback
between density (N ) and growth dN/dt. Thus, the most direct
way to illustrate population regulation is by showing the theoretical relationship
between these two variables:
2. Using the predictive form of the exponential growth equation, predict
population size in ten years of 150 turtles growing at 0.01 (1%) annual
per capita rate of increase. How long would it take the population to double
from 150?
The predictive solution to the exponential growth equation dN/dt
= rN is:
Nt = N0ert
…more easily solved as: lnNt = lnN0 + rt
Now we substitute, where N0 = 150; r = 0.01;
t = 10: lnN10 = ln150 + 0.01(10)
…which gives the answer lnN10 = 5.11, so N10
= 166 (rounded up)
Now, to solve for doubling time from 150 to 300, solve the equation
for t:
t = ( lnNt - lnN0)/r
t = 69+ years
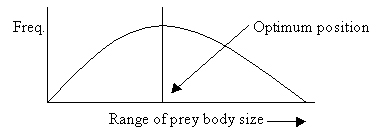
3. How does the Malthusian parameter r reflect an organism's
position in the fundamental niche? Show the position on a niche axis (your
choice) of an organism growing according to its biotic potential.
The parameter r can be interpreted as mean fitness for a population.
If the population is growing according to this biotic potential, most individuals
must be near the optimum position in the fundamental niche of that species.
For any given niche factor, there is a tolerance range, and the optimum
place on that range is defined as that which gives the best fitness, reflected
by the greatest frequency:
4. How fast is a logistic population of 40 individuals growing
if r = 0.02 and the carrying capacity of the environment is 250?
A logistic population has the sigmoid growth form generated by the
equation:
dN/dt = rN(1 - N/K)
…and the growth with the above numbers would be:
dN/dt = 0.02(40)(1 - 40/250)
= 0.67
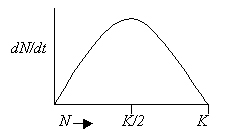
5. What is the significance of the inflection point on the logistic
growth curve? Show the inflection point on a graph where x = density and
y = dN/dt.
The inflection point, where Nt = K/2, is the point
at which the population replaces itself at the maximum rate, i.e.,
maximum dN/dt. This is the "maximum sustainable yield" for exploited
populations such as fish stocks, or the population density of pests that
is hardest to control.
6. What are the assumptions for logistic growth, and how realistic are
they?
Logistic growth assumes that a population will be responsive to the
carrying capacity of the environment ("K -recognition"), which is
an evolved trait that can be demonstrated in nature for real populations.
It also assumes that every individual added to the population has the same
impact on growth as every other individual, which implies that all individuals
take equal portions of the resource and that adding individuals at low
density has the same impact on growth as adding individuals at high density.
Since low density populations are unlikely to be resource limited, and
since different ages, sexes, and reproductive conditions of individuals
will cause variability in resource demand, these assumptions are unrealistic.
Finally, r and K are assumed to be constant. Biotic potential
may be constant over several generations, but carrying capacity of the
environment can vary stochastically in the short term. In spite of these
limitations, the logistic is a good ideal model with which to compare real
K - responsive populations, because deviations from the ideal sigmoid
growth curve can tell us which assumptions are violated.
7. What is the form of the global human population curve since the Middle
Ages? Explain how this came to be. What is global carrying capacity for
humans?
The growth curve of humans on a global scale has been exponential.
Much of this can be explained by raising the birth rate and carrying capacity
through agriculture and industry, and lowering death rate by improvements
in medical care. Establishment of a numerical value for global carrying
capacity is a thorny issue, but a reasonable standard of living would put
the value between one and two billion people, or about a third of the current
population size.
8. What is sexual selection, and how does the "handicap hypothesis"
fit into this idea?
The ability of an individual to choose a mate based on heritable behavioral
or morphological traits involved in mating behavior constitutes sexual
selection. It is like natural selection, in that an individual's fitness
depends upon how well it can attract a mate relative to others in the deme,
with mate choice being the selective agent. The handicap hypothesis assumes
that secondary traits that make one sex (usually male) more conspicuous
to the other also make it more attractive to predators. Thus, the female,
by choosing the conspicuous male, selects for a handicap in terms of escape
from predation.
9. What features of an oak tree are r-selected? Which features
are K-selected?
An oak tree is r-selected in that it has a large brood size
(seed set) and Type III survivorship. It is K-selected in that it
inhabits mature communities in which competition is important, has long
generation time and large body size.
10. Explain "parental investment."
Parental investment is the proportion of an organism's energy budget
expended on reproduction. It can involve expenditure on mating behavior
(courtship, territoriality, etc.), care of offspring, and number of offspring.
The trade-offs between semelparity and iteroparity can also be interpreted
as different strategies of parental investment: whether to put all your
eggs in "one basket" or to spread out reproduction over several breeding
seasons. These trade-offs are illustrated by the mathematical relationship
of brood size and age of first reproduction on the relative difference
between semelparity and iteroparity in terms of fitness (r).
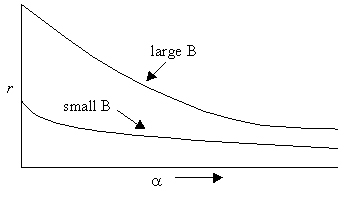
11. Explain and graphically illustrate on a single pair of axes
the relationships among age of first reproduction, brood size, and r
for an iteroparous organism.
The longer first reproduction is delayed the lower r
is, and the less difference brood size makes in r:
12. Define competition, and differentiate between interference and
exploitation.
Competition occurs when two or more organisms exploit the same,
limiting, resource. This interaction negatively affects all competitors,
but not necessarily to an equal degree (i.e., most competition is asymmetrical).
Competition can be intraspecific or interspecific. Interference occurs
when "access to a resource is limited by a the presence of a competitor"
(from Smith's text), which means both competitors are present at the same
time in the same place. This can result in "scramble" competition, in which
none of the participants is able to acquire sufficient resource to survive.
Exploitation, or "niche preemption," occurs when one competitor makes the
resource (usually space) unavailable to its competitors, usually by being
there before the others. Intraspecific competition is mainly by interference.
13. What is the Competitive Exclusion Principle? How does the notion
of guilds relate to this idea?
If competing species have identical resource requisites, eventually
the inferior competitor will go extinct. The greater the differences in
exploitation (methods or subsets of a resource), the lower the intensity
of competition. Guilds are groups of species that exploit the same class
of resources, but generally are to some degree dissimilar in their preferred
methods, area of foraging, or size class of resources. These differences
allow coexistence, but whether they arise as the "ghost of competition
past" or are merely preadaptive is usually undetermined.
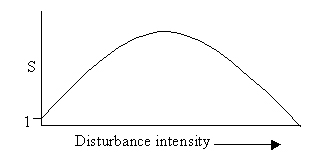
14. How does disturbance from predators or other extrinsic agents affect
competition, and what has this to do with the number of species that can
coexist in a community? Show this graphically.
Disturbance reduces competition, because it lowers population
densities of competing species relative to the amount of limiting resource
(i.e., makes the resource less limiting). The intermediate disturbance
hypothesis suggests there is an optimal level of disturbance that allows
a maximum number of potentially competing species to coexist. Less than
this level of intensity allows competition to reduce diversity; greater
than this level constitutes "overgrazing" which can cause extinction.
15. One of the outcomes of the Lotka-Volterra competition model is "either
species wins, depending." Depending upon what?
The outcome of competition can depend upon patterns in the
environment that may favor one species in one location, and the other in
another location; similarly, the environment may shift in time to favor
first one and then the other (e.g., seasonality, diurnality, etc.).
The outcome can also be affected by which species colonizes the resource
first, and how much time elapses before the others get there. An inferior
competitor can win an interaction if it is allowed to become well-established
with a large enough population before its competitors arrive.
16. What is a competitive network?
Competitive networks, sometimes called non-transitive competition,
are groups of species for which the outcomes of competition are not linear
or hierarchical. One species may outcompete a second species, the loser
may in turn win over a third species, but the third species can outcompete
the first. This may result from a difference in competitive strategies
and susceptibilities among species. It is uncertain how important this
kind of interaction is in nature; most demonstrations have involved space
as the limiting resource.
17. Explain how intraspecific and interspecific competition affect niche
width of a species population.
Intraspecific competition should force less fit members of
a population to seek sub-optimal resources, thus widening the repertoire
for the population as a whole: niche width increases. The mating system
of the grouse is an example, wherein less fit males are forced to display
for mates on the periphery of the optimal spatial position in the lek.
Essentially, intraspecific competition means there is not enough of the
optimal resource to go around, so inferior individuals must seek lesser
portions of that niche factor. Interspecific competition, by contrast,
produces greatest selection against sub-optimal individuals in the zone
of overlap among competing species; hence, niche width is decreased. The
shape of the resource niche at any given time thus depends on a balance
between these two opposing forces.
18. Write the general growth equation for one of two species in Lotka-Volterra
competition. Show and describe where intraspecific and interspecific competition
are accounted for.
The Lotka-Volterra equation is a simple modification of the
logistic equation to account for the effect of a second species on the
growth of the first. In the logistic, the term
(K-N)/K is a measure of intraspecific competition, because it
reflects the negative effect of increasing density on growth as density
gets closer and closer to carrying capacity. In order to measure the effect
of a second species, we need to correct for probably inequities in the
impact of different species on the resource, hence on the growth of the
first population. This is done by subtracting the number of individuals
of the second species, modified by a competition coefficient, a
= the relative impact of each individual of species 2 on the growth of
species 1:
dN1/dt = r1N1(1 - N1/K
- a N2/K)
19. (10 points!) Draw the competition isoclines and predict the outcome
of competition between species 1 (K = 250; a
= 1.4) and species 2 (K = 1,500; b =
0.9).
We first need the relationship between carrying capacities
and competition coefficients, in order to establish intercepts for both
axes:
K1/a = 179; K2/b
= 1666, so K1/a < K2
and K2/b > K1
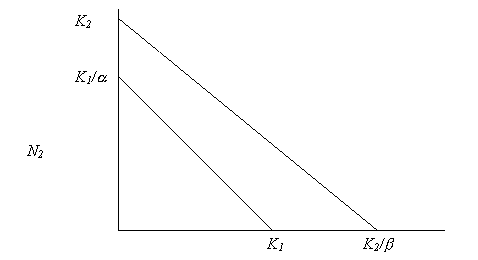
Since the isocline defining dN2/dt is everywhere
above the isocline for species 1, species 2 wins, no matter what the initial
conditions.





